Are you smart enough to work in Yandex?
Are you smart enough to work in Yandex?
Yandex is a large IT company. It was the first time I tried to attend it. I couldn’t even imagine that the interview consists of four sessions, each session is about one hour. You have to talk with four different people in four different places and solve lots of problems and answer the questions. In Yandex they used to write the codes on blank papers or just on the walls - this is very convinient. There are two major requirements you should carry about.
- Use an existing programming language to write your codes. You can use any language you prefer, but it can’t be a pseudo language.
- Your codes should be free of any compiler / interpreter errors.
The recipe of success is handling edge cases. The more problems you solve and the less syntax and / or logical mistakes you make, the higher you are.
In Yandex they believe that you have to have basic algorithmic knowledges. If you do, you can do anything else. I’ve failed my first attempt to join Yandex and decided to share some of the problems I faced during the interview.
The list of problems.
- Vertical line
- Two maximums
- Zip ints
- Count pairs
- Set difference
- FIFO queue
- Palindrome
- Reverse linked list
- Sum of diagonals
Vertical line
For given set of two-dimensional points check if a vertical line deviding the points symmetrically exists or not.
A pair of points (X1, Y1) and (X2, Y2) can be devided by a vertical line symmetrically if the equations X1 + X2 = C and Y1 = Y2 are held. If we find the other pair for which Y3 = Y4 is true, but X3 + X4 != C, we cannot devide this set of points by a vertical line symmetrically. And finnaly, if we don’t determine the constant C, we can’t devide the set too.
def check(points):
c = None
seen = {}
for x, y in points:
if y in seen:
if c:
if x + seen[y] != c:
return False
else:
c = x + seen[y]
else:
seen[y] = x
if c is None:
return False
return True
This algorithm takes O(n) time, but uses additional memory. In the worst case, when all the Ys are different, we will have a full copy of the source set of points requiring O(n) additional memory.
Two maximums
Find two maximums in unsorted array.
We can simply scan the array and check each value. Don’t forget about corner cases.
def get_maxs(values):
max1 = max2 = None
if not values:
return max1, max2
max1 = values[0]
if len(values) < 2:
return max1, max2
max2 = values[1]
if max1 < max2:
max1, max2 = max2, max1
for value in values[2:]:
if value > max1:
max2 = max1
max1 = value
elif value > max2:
max2 = value
return max1, max2
This algorithm takes O(n) time and O(1) additional memory.
Zip ints
For given array of non repeatable integers print a string of shortened sequences. For example, for array [4, 1, 2, 6, 3, 9, 7] the output is "1-4,6-7,9".
In order to find the sequences to compress it’s better to have the source array sorted. In a sequence for the previous element and for the current element the equation current = previous + 1 is held.
def zip_ints(values):
if not values:
return ''
sorted_values = sorted(values)
begin = end = prev = sorted_values[0]
zipped = []
for value in sorted_values[1:]:
if value == prev + 1:
end = value
elif begin < end:
zipped.append(f'{begin}-{end}')
begin = end = value
else:
zipped.append(f'{begin}')
begin = end = value
prev = value
if begin == end:
zipped.append(f'{begin}')
else:
zipped.append(f'{begin}-{end}')
return ','.join(zipped)
In Python built-in sorted method uses the Timsort algorithm to sort sequences. In the worst-case it takes O(n log n) time and O(n) additional space. Iteration through the sorted array takes O(n) time, thus the total time complexity of this algorithm is O(n log n).
Count pairs
A and B are sorted arrays. Count the pairs for which the equation a + b = x is held.
To solve the problem effectively, we have to scan both arrays in the same loop. The first array (A) we scan from the beginning down to the end (forward scan using i as an index), the second one (B) - from the end up to the beginning (backward scan using j as an index). There are three possible cases.
A[i] + B[j] < x- the sum is less thenx- we increase the sum by increasing the indexi(move forward along theAarray).A[i] + B[j] > x- the sum is more thenx- we decrease the sum by decreasing the indexj(move backward along theBarray).A[i] + B[j] = x- the sum is equal tox- we increase a count of found pairs. The number of increasing depends on the number of the same values placed together inAorB(sequences of the save values).
def get_count(a, b, x):
i = 0
j = len(b) - 1
total = 0
while i < len(a) and j >= 0:
if a[i] + b[j] < x:
i += 1
elif a[i] + b[j] > x:
j -= 1
else:
i += 1
count_a = 1
while i < len(a) and a[i] == a[i - 1]:
count_a += 1
i += 1
j -= 1
count_b = 1
while j >= 0 and b[j] == b[j + 1]:
count_b += 1
j -= 1
total += count_a * count_b
return total
The algorithm takes O(n+k) time and O(1) additional memory.
Set difference
A and B are sorted arrays. Find elements contained in A and not contained in B.
The problem is to find a set difference between A and B, but we have lists instead of sets. The lists are sorted, we can use that to find the result effectively.
def set_diff(a, b):
i = 0
j = 0
result = []
while i < len(a) and j < len(b):
if a[i] < b[j]:
result.append(a[i])
i += 1
elif a[i] == b[j]:
i += 1
else:
j += 1
result.extend(a[i:])
return result
We start processing A and B from the beginnig. We compare current elements. If we find, that an element from A is less, we will include it to the answer. Otherwise we move current positions i and j forward.
The loop terminates if all the elements from A or B are processed. If B is shorter, we have to add to the answer the rest elements from A starting from the current position.
This algorithm takes O(n+k) time and O(1) additional memory.
FIFO queue
Create a FIFO queue using two stacks.
FIFO queue is a queue where the oldest (first) item is processed first. In Python we have no special class for stacks, we can use lists instead.
The idea is to put incoming elements in the first stack. When the element is aquired, we have to turn the first stack and return an item from top of the second stack.
We can create a simple class that implements queue interface.
class FifoQueue:
def __init__(self):
self._instack = []
self._outstack = []
def enqueue(self, item):
self._instack.append(item)
def dequeue(self):
if not self._outstack:
self._turn()
return self._outstack.pop()
def _turn(self):
for _ in range(len(self._instack)):
self._outstack.append(self._instack.pop())
The usage of the FifoQueue class is simple. We have only 2 public methods. When we need to store data, the method enqueue is used. When we need stored data back, we call the dequeue method.
Palindrome
Check wheather a string is a palindrome or not. Non-alphanumeric characters are ignored. Case insensitive.
A palindrome - reading a word from left to right is equal reading a word from right to left. For example, ignoring the difference between uppercase and lowercase letters and skipping non-alphanumeric characters, the string Abcba! is a palindrome, while the string Hello is not.
Whereas there is a beautiful recursive solution, it takes additional memory per each recursion call and is not so effective as an iteration-based one.
def is_palindrome(s):
i = 0
j = (len(s) or 1) - 1
while i != j:
if not s[i].isalnum():
i += 1
continue
if not s[j].isalnum():
j -= 1
continue
if s[i].lower() != s[j].lower():
return False
i += 1
j -= 1
return True
This algorithm takes O(n) time and O(1) additional memory.
Reverse linked list
Reverse given linked list.
For that problem we need to define a new data type for linked list. For example, it may look like the following.
from typing import Any, NoReturn, Optional
class Node:
def __init__(self, value: Any, next: Optional['Node']) -> NoReturn:
self.value = value
self.next = next
Class Node defines a type for an item of the linked list. Each node has a payload (value of any type) and a pointer to the next node (the next attribute). If the node has no next node, we call it a tail node.
Using this data structure, a regular python list [1, 2, 3, 4, 5] can be represented like that.
tail = Node(5, None)
z = Node(4, tail)
y = Node(3, z)
x = Node(2, y)
head = Node(1, x)
The problem is to reverse given linked list, i.e. make tail node a head for the new linked list.
Usually we process such structures using iteration. For example, a function that prints linked list can be written like this.
def print_list(head: Node):
current = head
while current:
print(current.value)
current = current.next
Using such iteration pattern, we can walk through the list and swap the pointers of the two neighbour nodes.
def reverse(head: Node) -> Node:
previous = None
current = head
while current:
tmp = current.next
current.next = previous
previous = current
current = tmp
return previous
This algorithm makes changes in-place, i.e. it modifies an existing list. We can accept such behaviour for the sake of taking O(n) time and requiring O(1) additional memory.
Sum of diagonals
Find the sum of the diagonals of the square matrix.
In order to solve the problem, we need to sum all the diagonal elements. We call an element diagonal if it’s row index and column index are the same. Obviously, the algorithm has to take O(n) time to find the sum.
The first thing we should do is to understand how to process all the diagonal elements using only one loop iteration. For instance, let’s consider a square matrix of size 4.
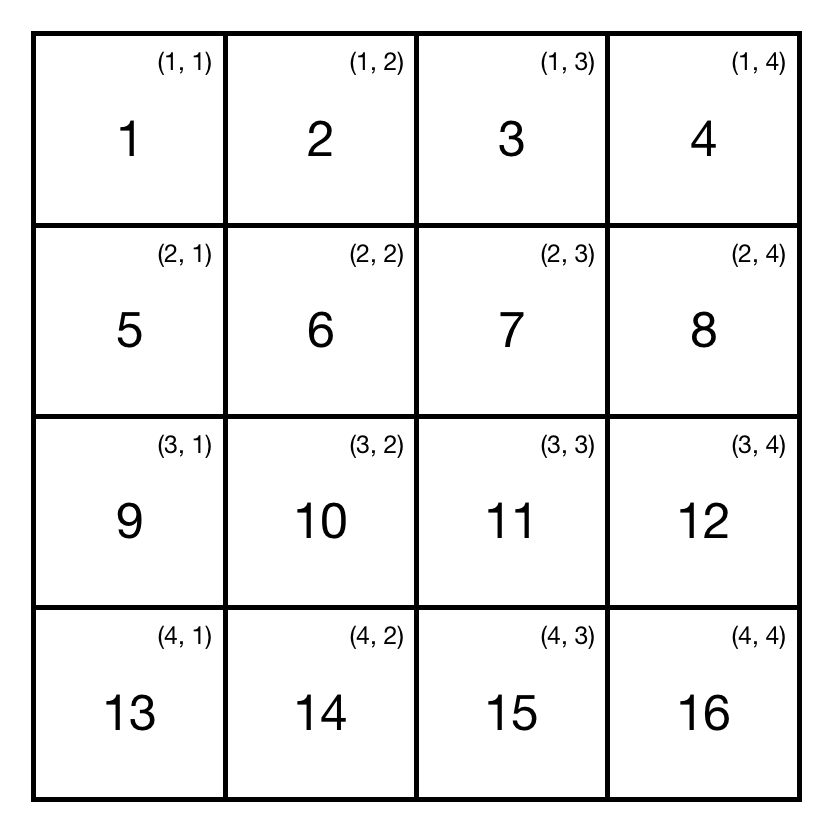
As we can see, in that case the sum is (1 + 6 + 11 + 16) + (4 + 7 + 10 + 13) = 68. The indices (X, Y) of the diagonal 1-6-11-16 are changing together from 1 up to 4. For the other diagonal 4-7-10-13 row X-index is changing from 1 up to 4, whereas column Y-index is changing from 4 down to 1. Keeping this in mind, let’s try to build the first version of the algorithm.
def get_diagonal_sum(matrix):
s = 0
n = len(matrix)
for i in range(n):
s += matrix[i][i] + matrix[i][n - i - 1]
return s
matrix = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16],
]
s = get_diagonal_sum(matrix)
print(s)
For our sample matrix this algorithm returns 68 and takes O(n) time. Let’s consider another example.
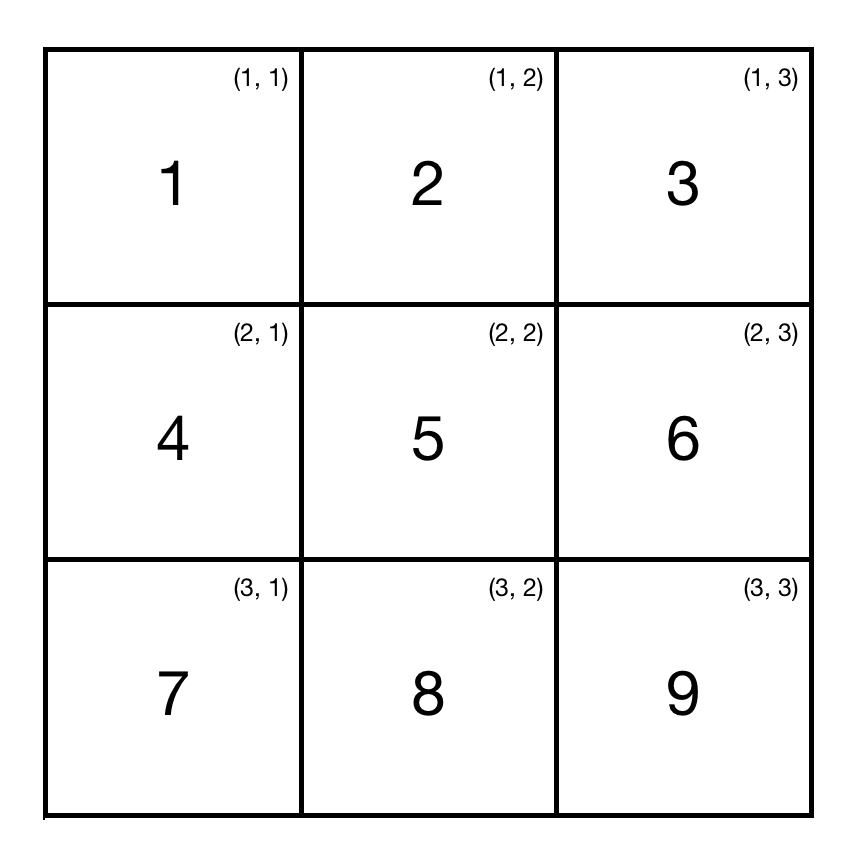
For that matrix the algorithm returns 30 instead of 25: central cell with value 5 is processed twice. Instead of making conditional check each loop iteration, we can subtract central cell before the result is returned.
def get_diagonal_sum(matrix):
s = 0
n = len(matrix)
for i in range(n):
s += matrix[i][i] + matrix[i][n - i - 1]
if n % 2:
i = int((n - 1) / 2)
return s - matrix[i][i]
return s
As you can see, now the algorithm returns correct result. This solution takes O(n) time and O(1) additional memory. The algorithm works for any other edge cases, e.g. matrices of 1 element or empty matrices.